Программирование недетерминированных игр

gordon0030@yandex.ru

Архив выпусков | Участники

Программирование недетерминированных игр

↓№ 263↑

03.06.2003 Хронометраж

50:09

Стенограмма эфира

Действительно ли шахматы являются самой интеллектуальной игрой, как это принято считать? Могут ли самообучаться игровые программы? В чем отличие недетерминированных игр от детерминированных с точки зрения программирования? О компьютерном моделировании творческих процессов — математики Борис Мельников и Алексей Радионов.

Участники:

Мельников Борис Феликсович — доктор физико-математических наук, профессор, заведующий кафедрой Теоретических основ информатики Ульяновского государственного университета

Радионов Алексей Николаевич — кандидат технических наук, доцент кафедры Теоретических основ информатики Ульяновского государственного университета

Обзор темы:

До сих пор не изжито представление о том, что можно создать искусственный интеллект как синоним искусственного разума. Но об этом и речи быть не может по целому ряду принципиальных соображений. Специалисты говорят исключительно об одном из важнейших направлений в информатике и математике, связанном с имитацией или моделированием на ЭВМ отдельных творческих процессов. Эта область науки мало интересуется тем, что происходит в человеческом мозгу, а занята построением ЭВМ и их программ, позволяющих воспроизвести отдельные процессы, по нашим человеческим оценкам — творческие.

Шахматист, делая тот или иной ход, может руководствоваться прецедентами, прошлым опытом, умением, интуицией, догадкой, просмотром на сколько-то ходов вперед. Не все это формализуется. Зато мы в точности знаем, как это делает ЭВМ, так как человек составил для нее программу-инструкцию, позволяющую количественно оценивать ту или иную ситуацию. В машине играет в шахматы не программа, а тот человек, который сумел формализовать шахматную игру и составить программу.

Рассмотрим некоторые эвристики, применяемые при программировании игр — естественно, речь идет об интеллектуальных играх, а не о значительно более популярных в настоящее время динамических играх, рассчитанных, в первую очередь, на быстроту реакции пользователя, и лишь во вторую (или даже в последнюю) — на его интеллект. Эвристики — это специальные методы, используемые в процессе открытия нового. Второе значение термина «эвристика» — наука, изучающая продуктивное творческое мышление.

В качестве типичного примера интеллектуальной игры чаще всего называют шахматы. И это не случайно — при программировании огромного количества интеллектуальных игр используются те же самые модели, что и в шахматах. Математическое исследование этих моделей, обобщение накопленного к концу 70-х годов опыта уже сделано, а то, что было создано впоследствии, пока еще нуждается в подобном фундаментальном труде.

По мнению Б. Ф. Мельникова, в литературе, посвященной искусственному интеллекту вообще и программированию интеллектуальных игр в частности, шахматам (и «аналогичным’ простым играм) уделено слишком большое внимание. Более того, о шахматах утвердилось мнение как о самой интеллектуальной игре, когда-либо изобретенной человеком. Математики проводят аналогии между мышлением шахматиста и математика, экономисты говорят о помощи шахматного мышления для работы „на рынке ценных бумаг“, психологи — о его помощи в разных жизненных ситуациях... Однако Б. Ф. Мельников придерживается особого мнения. Он считает, что человечество сделало ошибку, назвав именно шахматы самой интеллектуальной игрой. Ученый считает такой игрой Backgammon, почти не отличающийся от известной в России (и других странах бывшего СССР) игры „короткие нарды“. При игре в Backgammon человек занимается не только прямым пересчетом, но и — в значительно большей степени, чем при игре в шахматы — качественной оценкой позиции; за последнюю же, по-видимому, „отвечает“ правое полушарие мозга — следовательно, оба полушария в этом случае „задействованы“ полностью.

Все-таки шахматы не случайно так часто упоминаются. При программировании огромного количества интеллектуальных игр используются те же самые модели, что и в шахматах. Среди таких игр можно назвать реверси, калах, оуа, рэндзю, разные (национальные) версии шашек. Стоит еще упомянуть различные игры, рассматривавшиеся М. Гарднером — в заметках, публиковавшихся в течение нескольких десятилетий в журнале „Scientific American“, а также в его книгах, некоторые из которых переведены и на русский язык. Большинство указанных игр — детерминированные; таковых в упомянутых книгах несколько десятков, тогда как недетерминированных — существенно меньше. Отметим, однако, что не во всех детерминированных играх можно использовать „шахматные“ модели, эти модели неприменимы при игре в го (эту игру часто неудачно называют японскими шашками).

В различных национальных версиях шашек, для получения очень сильных программ часто достаточно использовать те же самые модели, что и в шахматах, но в значительно более простом виде. Например, программы разных версий 64-клеточных шашек обыграли действующих чемпионов мира в 60-х годах, что на 30 и более лет раньше, чем в шахматах. Кроме того, многие из методов дискретной оптимизации в задачах программирования недетерминированных интеллектуальных игр, которые будут описаны ниже, могут быть применены и в „обычных“, детерминированных играх. Кроме того, эти же методы применяются автором и в других задачах искусственного интеллекта.

Карточные игры — причем все — в советское время были отнесены к „азартным“; при этом многие из них (в первую очередь такие недетерминированные игры как преферанс и бридж) совершенно несправедливо. К сожалению, это отношение перешло и на отечественные работы, связанные с программированием игр.

Итак, обзор посвящен прежде всего эвристикам, применявшимся в программировании недетерминированных игр — и поэтому (в связи с наличием эвристик, желательность применения которых практически невозможно доказать строго) может быть раскритикован представителями чистой математики. Однако, в настоящее время подобная ситуация прослеживается практически во всех областях искусственного интеллекта.

Динамическая оценка позиции. В чем же главное отличие недетерминированных игр от детерминированных с точки зрения программирования? В том, что дерево игры, построенное для первых, включает не только вершины, в которых игрок должен выбрать конкретный ход, но и другие — те, в которых ему следует ожидать некоторой конкретной реализации случайного события. Поэтому метод минимакса при программировании перебора в недетерминированных играх приходится обобщать.

Будем исходить из предположения автора, что сам „канонический“ метод минимакса читателю известен. В недетерминированных играх чередуются: конкретная реализация некоторого случайного события, ход одной из сторон, снова реализация случайного события, ход другой стороны. Количество всевозможных исходов случайного события должно быть конечным (иначе придется применять другие модели). В результате в дереве игры появляются уровни, заключенные между уровнями очередности ходов соперников. Эти новые уровни отражают те моменты игры, в которые реализуется исход случайного события. Обобщение метода минимакса работает именно с таким деревом.

Итак, считаем, что мы умеем строить статическую оценку позиции. Временным удалением недетерминированности получаются предварительные оценки позиций дерева игры. Для этого мы сначала предполагаем, что уже реализовался конкретный исход случайного события, и вычисляем динамическую оценку для данной позиции так же, как и в „обычном“ методе минимакса. Затем вычисляем динамическую оценку позиции для следующего исхода случайного события, и так далее для всех исходов.

Окончательная динамическая оценка позиции определяется на основе всех детерминированных оценок, полученных для всех возможных значений случайного события. Полученные значения детерминированных (обычно — статических) оценок специальным образом усредняются — это и есть окончательная динамическая оценка. С физической точки зрения такое усреднение дает положение центра тяжести одномерной системы тел с массами, определяемыми специально подобранной функцией (функцией риска). Координаты тел системы — значения соответствующей детерминированной оценки, которая определяется только детерминированными факторами игры, как, например, в обычном минимаксе. Например, пусть a₁,..., a_k — значения детерминированных оценок, а f — некоторая функция риска. Тогда значение динамической оценки вычисляется по следующей формуле:

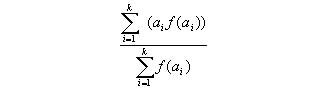
(SUM(i=1..k) ai*f(ai)) / (SUM(i=1..k) f(ai))

Даже программа, написанная только на основе этого обобщения и имеющая самую тривиальную функцию статической оценки позиции, давала неплохие результаты — обыгрывала многие (но не все) программы. Но такие результаты, конечно же, нельзя назвать очень хорошими. В дальнейшем программа постепенно улучшалась. По мнению Б. Ф. Мельникова, все работы по улучшению можно было кратко охарактеризовать следующим образом: в них оптимизировался какой-либо способ вычисления статической оценки позиции. Автор пошел иным путем — и некоторые из направлений улучшения программы, примененные после введения простейшей динамической оценки, описаны ниже.

Автоматическая смена стратегии. Отметим, что описанные далее приемы и алгоритмы могут быть реализованы, например, с помощью нейросетей. Однако в данном случае используемые здесь алгоритмы позволяют обходиться и без них, существенно упрощая работу практического программирования. Материал этого пункта не связан с автоматическим изменением набора правил, применяемых при выборе очередного хода, — работа над этой темой является задачей обозримого будущего. Однако название раздела не является преувеличением: изменение специальных коэффициентов — не являющихся коэффициентами статической оценки позиции — действительно приводит к изменению стратегии игры программы.

Перед описанием таких алгоритмов рассмотрим немного подробнее, почему обобщение метода минимакса для недетерминированных игр действительно стоит формулировать именно так, как это сделано в разделе „Динамическая оценка позиции“. Покажем, что это обобщение следует из реального мышления игрока, проявляющегося далеко не только в какой-либо недетерминированной игре, но и, по большому счету, в иных различных жизненных ситуациях. Действительно, человек чаще всего не самые удачные реализации случайных факторов (в backgammon’e это варианты бросков кубиков противника) должен считать более вероятными, чем хорошие для него: надо быть хоть немного, да пессимистом. То есть усреднение, кратко описанное выше, необходимо делать с весами тем меньшими, чем более „хорошим для нас“ является будущее показание кубиков противника (повторим: так надо делать не всегда, но чаще всего).

Возникает вопрос: насколько надо уменьшать веса для „хороших для нас“ показаний кубиков противника? Если заранее задать функцию риска и употреблять ее независимо от каких-либо иных обстоятельств с простейшей функцией статической оценки позиции, то даже в этом случае результаты получаются довольно хорошими. Автором при этом были рассмотрены различные убывающие функции риска. Простейшее интуитивное объяснение того, что обычно функция риска должна быть убывающей, можно рассматривать как выход из следующего небольшого статистического исследования Гарднера: человек за возможность сыграть в простейшую игру, заключающуюся в подбрасывании монеты и получении 10 долл. в случае выпадения орла, в среднем готов заплатить 3–4 долл. (но не 5).

Итак, для получения более сильной программы необходимо проводить смену стратегий в процессе игры. Один из путей улучшения простейшей динамической оценки позиции заключается в следующем. Мы можем заранее прикинуть оценку позиции (т. е. как примерно мы „стоим“ — на выигрыш или совсем наоборот); далее: если мы выигрываем или „проигрываем совсем мало“ — то надо быть пессимистами, и примерный вид функции риска описан выше (убывающая); если „проигрываем больше“ — то функция риска близка к константе; если же „проигрываем сильно“ — то, наоборот, функция риска является возрастающей: ведь в этом случае необходимо быть сверхоптимистами и надеяться почти на чудо (а что делать?).

Есть много промежуточных вариантов этих функций риска. Она может быть значением статической оценки позиции, а может быть значением динамической оценки, полученным при применении простейшей функции риска. Обозначим ее S. Применение динамической функции риска может быть проведено более одного раза. Например, для первого шага S является значением статической оценки позиции (или значением динамической оценки с простейшей функцией риска, равной константе), а для каждого следующего шага S является значением динамической оценки, найденной на предыдущем шаге. И именно, исходя из такого значения S, выбирается конкретная функция риска для данного шага. Такое повторение может улучшить динамическую оценку позиции, поскольку конкретная функция риска выбирается на основе все более достоверной априорной информации. Более того, при выполнении конкретной программы на компьютере это повторение не занимает много времени, поскольку основное время работы процессора тратится на вычисление именно статических оценок (аналогичный факт верен и для случая детерминированных игр). Однако, как показала практика, применять этот прием более 3–4 раз не имеет смысла.

Далее, функции, приведенные выше, удобно описывать с помощью трех параметров — например, параметров, являющихся значениями функции риска в точках 0, 0,5 и 1 — при этом сама функция риска строится с помощью квадратичной интерполяции. Для дальнейшего удобно обозначать эти три функции — как функции от статической (или простейшей динамической) оценки S — записью f_s(0), f_s(0,5), f_s(1).

Данные параметры можно выбрать таким образом, чтобы интерполирующие функции для нескольких значений S оказались близкими к выбранным выше. Первый и третий параметры f_s(0) и f_s(1), характеризуют изменение функции риска (при росте S) от возрастающей к убывающей. А второй параметр, f_s(0,5), характеризует изменение выпуклости функции риска при росте S. Последние три функции также можно считать зависящими от параметров.

Основные эвристики процесса самообучения игровых программ. „Турнирные“ алгоритмы самообучения». Самообучение можно рассматривать как повторяющиеся игры программы с самой собой, при этом два играющих варианта одной и той же программы используют немного отличающиеся друг от друга множества коэффициентов (последние применяются просто для статической оценки позиции). Таким образом, «силу программы» можно рассматривать как функцию многих переменных. Однако — какую именно функцию? Этот вопрос в литературе (как в статьях, так и на интернетовских страницах) практически не отражен; предполагается, что если одна программа (точнее — один набор коэффициентов) выиграла у другой (другого), то и значение такой функции на первом наборе коэффициентов больше.

Однако даже при этом предположении оптимизировать подобную функцию силы программы крайне сложно, так как она имеет большое количество локальных максимумов; кроме того, по-видимому, даже в некоторой локальной области невозможно исследовать подобную функцию на выпуклость. Еще большие проблемы, связанные с самим определением такой функции силы, вызывают «нетранзитивные наборы коэффициентов». Хотя, заметим, самые простые методы поиска экстремума (автор в практическом программировании часто пользуется модификацией градиентного метода с неявным вычислением частных производных) дают неплохие практические результаты — несмотря на описанные здесь и далее проблемы, связанные с определением функции силы.

При подобном самообучении все авторы считают очевидным тот факт, что результатом самообучения должен быть набор коэффициентов, на котором у программы значение функции силы (кратко охарактеризованной выше) максимально возможное. Однако — почему более важна именно такая программа, «объективно более сильная»? Разве не опровергают эту мысль многочисленные примеры нетранзитивных игр? Интересно заметить, что и в реальной жизни, в самых разных игровых видах спорта, встречались и встречаются ситуации, когда в соревновании в итоге побеждает далеко не сильнейший (но общему признанию) участник. Конечно, частая причина этого — несовершенство системы проведения соревнований; кстати, статистическое исследование систем (как уже существующих, так и потенциально возможных), сравнение их по различным критериям — тема отдельного небольшого исследования. Однако часто в реальной жизни встречаются и другие причины. Например, А. Алехин в международных шахматных соревнованиях 30-х годов постоянно проигрывал Л. Асталошу, шахматисту практически неизвестному и ничем иным не прославившемуся.

Итак, почему для пользователя нужнее «объективно более сильная» программа — т. е. почему именно такая программа должна стать «результатом» процесса самообучения? Ведь играть-то этой программе чаще всего предстоит вовсе не с «абсолютным» противником, неошибающимся супер-чемпионом, а с реальным — и неважно, с человеком или с какой-либо другой программой. И именно с таким «усредненным» соперником наша программа должна показать хорошие результаты — настолько хорошие, насколько позволит процесс самообучения. Обобщая, скажем, что игровая программа должна показать свое превосходство не против какой-либо одной (пусть даже очень сильной) программы, а против нескольких, среди которых встречаются и не самые сильные.

Немного упрощая ситуацию, можно сказать, что для выбора одной игровой программы из нескольких мы должны провести турнир между ними. (И, также упрощенно, определить силу программы как случайную величину, реализация которой — результат выступления этой программы в турнире.) Но по какой именно системе, по каким именно правилам следует проводить турнир? Как понятно из вышеизложенного, даже в турнире по круговой системе (не говоря уже о совсем необъективной олимпийской) может показать более хорошие результаты программа, которая иногда применяет не самые сильные ходы. То есть даже в детерминированных играх возможен выбор из двух ходов, один из которых более сильный, зато другой — с риском, «ловушкой? Тем более это верно для недетерминированных игр, где риск может быть строго определен. Риск может быть определен при условии, что единственная цель — выиграть одну партию в короткие нарды (backgammon). Однако даже в последней игре существуют ситуации, когда эта цель не является самой важной в данный момент (хотя этот факт и может показаться довольно странным для шахматиста, специалиста но шахматному программированию и т. п.). Например, такая ситуация иногда возникает при проведении матча с использованием удваивающего куба (cube) — а ведь именно таким образом обычно проходят официальные соревнования по backgammon’y.

Автор при практическом программировании самообучения применял разные системы. По понятным причинам, олимпийская система плоха; поэтому нередко применялись круговая система (когда каждая программа встречается с каждой, и победитель определяется по общему числу побед).

Но и круговая система не является оптимальной, она имеет, по крайней мере, следующие четыре недостатка.

1. Временные ограничения: необходимо провести очень большое число партий (матчей).

2. В очень большом проценте партий встречаются один из сильнейших участников с одним из слабейших — так что даже в случае недетерминированных игр исход часто предрешен заранее.

3. Наоборот — много партий (между двумя слабыми участниками) никак не влияют на конечный результат процесса самообучения. Особенно часто такая ситуация встречается при большом количестве программ-участниц, а их в некоторых случаях бывает очень много — например, когда мы допускаем большой разброс возможных коэффициентов набора.

4. Несмотря на сказанные выше слова, что итоговая (искомая) программа должна показать свое превосходство не против какой-либо одной программы-соперницы, а против нескольких, с более сильными программами желательно играть чаще.

И чем изобретать некоторый критерий, преодолевающий эти недостатки (например, усредняя результаты встреч с некоторыми весами, — этот критерий в чем-то аналогичен функции риска), — лучше воспользоваться уже имеющимся готовым рецептом, так называемой швейцарской системой проведения турнира.

Основные положения швейцарской системы кратко опишем и в данном обзоре. В классическом варианте этой системы обычно предполагается, что число участников N довольно велико, а число туров (т. е. партий, проводимых каждым участником) значительно меньше числа N-1, нужного для проведения круговой системы, и лишь немногим (обычно примерно в 2 раза) превышает число [log₂N]+1, нужное для проведения олимпийской системы. В каждом туре составляются пары из участников, имеющих равное (или примерно равное) число очков; при этом повтора пар не допускается. Из приведенного краткого описания швейцарской системы видно, что при этом преодолеваются три из четырех ранее описанных недостатков круговой системы. И действительно, многолетняя практика применения швейцарской системы в шахматных соревнованиях показывает ее «живучесть» (поскольку шахматисты-практики дают о ней, в основном, положительные отзывы). Однако один недостаток остается (большое число партий, не влияющих на итоговый результат процесса), поэтому Б. Ф. Мельников при практическом программировании самообучения чаще всего применял модификации швейцарской системы.

Основное в этих модификациях — то, что после каждого проведенного тура определенный процент программ-участниц, занимающих последние места, либо (в простом варианте системы) выбывает из турнира, либо (в более сложном варианте) заменяется на «более перспективные». При этом во втором варианте необходимо постоянно генерировать некоторое число новых участников турнира (процесса), т. е. новые наборы коэффициентов. Наиболее естественный путь генерации таких новых наборов коэффициентов — создание специальных модификаций генетических алгоритмов. Отметим еще, что в связи с недетерминированностью рассматриваемых игр результаты разных партий двух выбранных наборов коэффициентов различны — поэтому тур для уменьшения влияния случайных факторов удобно делать состоящим не из одной партии, а из нескольких (и партия превращается в матч).

Программист или игрок-эксперт может с увлечением следить за «ходом» подобного турнира. Турнир программ проходит весьма напряженно, среди лидеров встречаются программы «с разными характерами»: например, одна из них «понемногу» у всех выигрывает (немногим более 50% партий, зато практически у всех), другая может «по крупному» выиграть (у программы, которая, казалось бы, примерно равна ей по силе), но может и неожиданно проиграть. (По-видимому, именно на подобной паре программ наиболее четко прослеживается возможность изменения не только тактики игры, но и стратегии, с помощью изменения коэффициентов оценки позиции.) Как упорядочить по силе две такие программы? Какой набор коэффициентов занести в финальную версию алгоритма? Именно на этот вопрос и отвечают «турнирные» алгоритмы самообучения, кратко описанные выше.

Другие алгоритмы самообучения и связанные задачи. При организации самообучения программ автором применялся следующий алгоритм для локальной сети ЭВМ. Набор коэффициентов, «лидирующий» в турнире, имеет б́ольший приоритет (б́ольшую вероятность) для назначения его на следующую партию (матч); это назначение выполняется головным компьютером для проведения на каком-либо ином компьютере сети. Может быть, математик позаимствовал подобный приём у шахматной программы «Deep Thought», обыгравшей Г. Каспарова (однако там он применялся для организации взаимодействия процессов, выборе более перспективного из них — да и всех своих «тайн» авторы той программы ещё не открыли). По-видимому, эта тема ещё ждёт дальнейшего развития, схожие алгоритмы (самообучения в локальной сети) могут применяться и в других задачах дискретной оптимизации, не связанных с задачами игрового программирования.

Рассмотрим ещё один приём — настройку программы при самообучении на конкретного противника. (Отметим, что такая группа алгоритмов может быть отнесена к алгоритмам автоматического изменения стратегии.) В процессе обдумывания хода соперником программа пытается определить «его алгоритмы обдумывания» (при этом не важно, кто играет против неё — человек или другая программа), подстраивая под предыдущие ходы, сделанные им (в том числе — его ходы в предыдущих партиях), некоторый набор коэффициентов, и находя, какой именно набор наиболее точно отражает предыдущие ходы этого противника. Далее этот набор коэффициентов применяется при анализе в глубину наряду с другим, «виртуальным противником», и при различии возможных ответов им обоим уделяется особое (т. е. отражаемое б́ольшим значением весового коэффициента) внимание при переборе. Резюме: программа должна (и может) применять с разными соперниками немного различающиеся модели игры. Кроме того, даже в самих коммерческих игровых программах ст́оит не просто вводить разные уровни игры, а, более того, разные стратегии — кому из пользователей что понравится.

Последний из применявшихся при самообучении алгоритмов связан с упомянутым в предыдущем абзаце «виртуальном противником» — т. е. с подпрограммой, предлагающей ответные ходы за противника после некоторого нашего хода; эти ответные ходы используются при переборе ходов. Во многих работах, причём посвящённых не только детерминированным играм, но и недетерминированным в качестве такового рассматривалась только копия нашей программы (имеющая, конечно же, меньшее значение для максимально возможной глубины перебора). Однако при описанном выше самообучении в турнире и доступности всех подпрограмм для любой другой из них в качестве такого «виртуального противника» удобнее применять либо набор коэффициентов самой программы-противника, либо тот набор, который в данный момент «лидирует в турнире». (Особо отметим, что рассмотренный в этом абзаце приём ничего общего не имеет с описанной выше большей вероятности выбора «лидирующего» в турнире набора коэффициентов для формирования очередной пары противников.)

Заключение. Самое интересное между «да» и «нет». Основным результатом работы Б. Ф. Мельникова по данной теме является программа игры в backgammon (короткие нарды), обыгрывающая как всех известных автору игроков-практиков, так и все программы, найденные в Интернете и других источниках. По его мнению, backgammon — не только самая интеллектуальная игра, но и более, чем шахматы, интересен для создания игровых программ. К этому необходимы сразу несколько замечаний. Название «backgammon» лучше записывать латинскими буквами, так как применяющаяся иногда русская интерпретация этого названия — бэкгэммон — «смотрится» ещё хуже. Небольшие отличия backgammon’а от коротких нард всё же есть, поэтому ниже название «нарды» здесь не употребляется. С точки зрения программирования можно было бы выбрать любую из двух моделей — автор выбрал более распространённый backgammon, имеющий, кстати, международную федерацию, наподобие шахматной. И, по-видимому, отечественным любителям нард ст́оит перейти на международный стандарт. Короткие нарды ни в коем случае не надо путать с длинными, которые вряд ли стоит считать интеллектуальной игрой. Последние — просто «передвигание фишек» в соответствие с показаниями двух кубиков, и в этой игре в партии более-менее опытных игроков практически всегда в итоге побеждает тот, чьи показания в сумме оказались больше. Б. Ф. Мельников действительно считает backgammon более интеллектуальной игрой, чем шахматы. Однако «квасным патриотом» backgammon’а его, по-видимому, назвать нельзя: он имеет не только «математические регалии», но и — не намного меньшие — именно шахматные. Вообще, среднее число возможных ходов в backgammon’е, (после того, как уже стало известно конкретное показание кубиков), по-видимому, примерно равно среднему числу возможных ходов в шахматах (т. е. примерно 25–40 вариантов). Более того, несложно привести пример, когда число возможных ходов в позиции backgammon’а превышает максимальное возможное число ходов в шахматной позиции, равное 10⁹.

Прослеживается большая аналогия между парой шахматы / backgammon с одной стороны, и парой классическая / нечёткая логика — с другой. Приведём по этому поводу мысль из книги математика и философа Барта Коско (Bart Kosko) «Fuzzy Thinking» («Нечёткое мышление») — она цитируется по одному из многочисленных пересказов этой книги, имеющихся в Интернете. Коско считает, что два тысячелетия назад человечество сделало роковую ошибку, заложив в фундамент науки не «зыбкую поэтику ранних восточных философий», а «выхолощенную двоичную логику Аристотеля». И с тех пор классическая «чёрно-белая» бинарная логика всё более отдаляется от реального многоцветного мира, где нет ничего абсолютного, а всё самое интересное «происходит в туманной области между „да“ и „нет“».

Методы, применявшиеся при создании программы и самообучении игровых программ, могут найти применение (и уже находят) во многих других задачах дискретной оптимизации и искусственного интеллекта. Среди этих задач и очень часто встречающаяся задача о подборе наилучших параметров при имитационном моделировании стохастических процессов. Один из примеров — задача теории биологических популяций (без статистики старения). В последнем случае прослеживается очень большая аналогия с недетерминированными играми. Действительно, при одних и тех же входных параметрах возможны различные варианты изменения параметров популяции в зависимости от времени — в этом и проявляется недетерминизм. Однако параметры имитационного моделирования, несмотря на недетерминизм, должны быть подобраны статистически наилучшим образом.

Рассмотренный подход имеет аналогии в других задачах, например: при моделировании экономических процессов, краткосрочном прогнозировании микро- и макроэкономических параметров, в теории принятия решений с использованием алгоритмов нечеткой классификации ситуаций и др.

Библиография

Адельсон-Вельский Г.М., Арлазаров В. Л., Донской М. В. Программирование игр. М., 1978

Ботвинник М. М. Алгоритм игры в шахматы. М, 1968

Гарднер М. Математические досуги. М., 1995

Клемент Р. Генетические алгоритмы: почему они работают? когда их применять?//Компьютерра. 1999. № 11

Лернер А. Я. Начала кибернетики. М., 1967

Мельников Б. Ф., Мосеев А. В. Недетерминированные игры и экономика/Математические методы и компьютеры в экономике: Сборник материалов конференции. Пенза, 1999

Мельников Б. Ф., Радионов А. Н. О выборе стратегии в недетерминированных антагонистических играх//Программирование: Изв. РАН. 1998. № 5

Мельников Б. Ф. Эвристики в программировании недетерминированных игр//Програмирование: Изв. РАН. 2001. № 5

Мельников Б. Ф., Романов Н. В. Ещё раз об эвристиках для задачи коммивояжёра//Теоретические проблемы информатики и ее приложений. Саратов, 2001. Вып. 4

Нейман Дж. фон. Теория игр и экономическое поведение. М., 1970

Цермело Э. О. Применении теории множеств к теории шахматной игры/Матричные игры. М., 1961

Шеннон К. Э. Играющие машины/Работы по кибернетике и теории информации. М., 1956

Berliner H. Computer backgammon//Scientific Am. 1980. № 243

Zbigniew M., Michalewicz S. Genetic algorithm + Data stucture = Evolution programs. Berlin; Heidelberg, 1992

Melnikov B. A new algorithm of the state-minimization for the nondeterministic finite automata//The Korean Journal of Computational and Applied Mathematics. 1999. V. 6. № 2

Melnikov B. Once more about the state-minimization of the nondeterministic finite automata//The Korean Journal of Computational and Applied Mathematics. 2000. V. 7. № 3

Тема № 263

Эфир 03.06.2003

Хронометраж 50:09

www.ntv.ru

Сайт управляется системой uCoz